直方图
直方图的简介
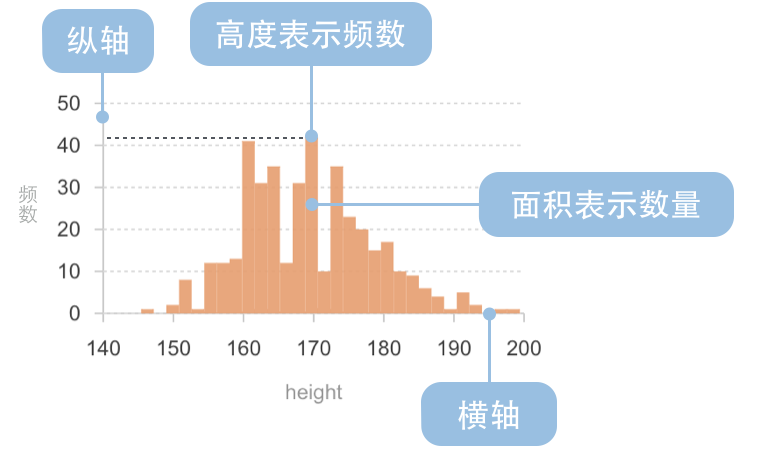
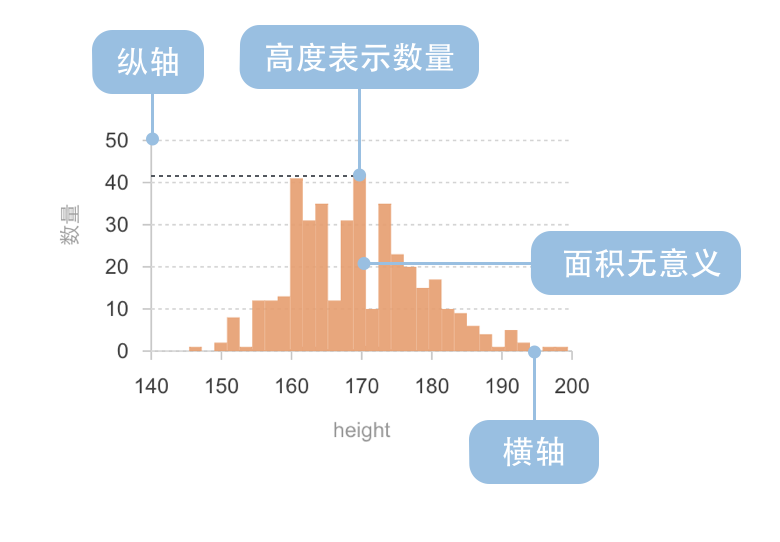
直方图,形状类似柱状图却有着与柱状图完全不同的含义。直方图牵涉统计学的概念,首先要对数据进行分组,然后统计每个分组内数据元的数量。 在平面直角坐标系中,横轴标出每个组的端点,纵轴表示频数,每个矩形的高代表对应的频数,称这样的统计图为频数分布直方图。频数分布直方图需要经过频数乘以组距的计算过程才能得出每个分组的数量,同一个直方图的组距是一个固定不变的值,所以如果直接用纵轴表示数量,每个矩形的高代表对应的数据元数量,既能保持分布状态不变,又能直观的看出每个分组的数量。本文的例子全部使用纵轴表示数量的非标准直方图绘制。
相关概念:
- 组数:在统计数据时,我们把数据按照不同的范围分成几个组,分成的组的个数称为组数
- 组距:每一组两个端点的差
- 频数:分组内的数据元的数量除以组距
直方图的作用
- 能够显示各组频数或数量分布的情况
- 易于显示各组之间频数或数量的差别
通过直方图还可以观察和估计哪些数据比较集中,异常或者孤立的数据分布在何处
英文名:Histogram
直方图的构成
频数分布直方图
| 图表类型 | 直方图 |
|---|---|
| 适合的数据 | 列表:一个连续数据字段、一个分类字段(可选) |
| 功能 | 展示数据在不同区间内的分布情况 |
| 数据与图形的映射 | 分组数据字段(统计结果)映射到横轴的位置 频数字段(统计结果)映射到矩形的高度 分类数据可以设置颜色增强分类的区分度 |
| 适合的数据条数 | 不低于 50 条数据 |
非标准的直方图
| 图表类型 | 直方图 |
|---|---|
| 适合的数据 | 列表:一个连续数据字段、一个分类字段(可选) |
| 功能 | 展示数据在不同区间内的分布情况 |
| 数据与图形的映射 | 分组数据字段(统计结果)映射到横轴的位置 数量字段(统计结果)映射到矩形的高度 分类数据可以设置颜色增强分类的区分度 |
| 适合的数据条数 | 不低于 50 条数据 |
直方图的应用场景
适合的场景
例子1: 用于表示分布情况
以统计学中经典的鸢尾花案例为例,其数据集包含了 50 个样本,都属于鸢尾属下的三个亚属,分别是山鸢尾、变色鸢尾和维吉尼亚鸢尾。四个特征被用作样本的定量分析,它们分别是花萼长度、花萼的宽度、花瓣的长度和花瓣的宽度。基于这四个特征的集合,费雪建立了一种线性判别分析法以确定其属种。
| SepalLength(花萼长度) | SepalWidth(花萼宽度) | PetalLength(花瓣长度) | PetalWidth(花瓣宽度) | Species(属种) |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| ... | ... | ... | ... | ... |
| 7.0 | 3.2 | 4.7 | 1.4 | versicolor |
| 6.4 | 3.2 | 4.5 | 1.5 | versicolor |
| ... | ... | ... | ... | ... |
| 6.3 | 3.3 | 6.0 | 2.5 | virginica |
| 5.8 | 2.7 | 5.1 | 1.9 | virginica |
| ... | ... | ... | ... | ... |
例子2: 用于观察异常或孤立数据
下图绘制了钻石的全深比数据的统计直方图,从图中可以看出在 66 附近有两个孤立值
| name(钻石名称) | depth(全深比) |
|---|---|
| 14513 | 61.4 |
| 28685 | 64 |
| 50368 | 59.2 |
| ... | ... |
不适合的场景
抽取的样本数量过小,将会产生较大误差,可信度低,也就失去了统计的意义。因此,样本数不应少于 50 个。
直方图的扩展
通过变换坐标系,我们能获得极坐标下的直方图、圆环上的直方图、以及翻转的直方图。
直方图与其他图表的对比
直方图与柱状图
- 柱状图是以矩形的长度表示每一组的频数或数量,其宽度(表示类别)则是固定的,利于较小的数据集分析。
- 直方图是以矩形的长度表示每一组的频数或数量,宽度则表示各组的组距,因此其高度与宽度均有意义,利于展示大量数据集的统计结果。
- 由于分组数据具有连续性,直方图的各矩形通常是连续排列,而柱状图则是分开排列。
